Software Renderer Tutorial - Clipping

So far the engine behaves as expected when objects are in front of the camera. When an object goes behind or through the camera however, it can cause our renderer to crash or lag. As an example, we will scoot the scene from the previous example slightly closer to the camera so that the moving plane goes through and behind the camera’s view point and near clipping plane. I have provided the lines from the previous example that I have modified below:

let zOffs = Math.sin(val*2.5) - 1;

let translate2 = Mat4.translate(0, 0, -1);

The modifications above will run smoothly until the plane gets close to the camera. When part of the plane goes behind the camera, the renderer gets so slow that it appears to freeze. What could be causing this slow down? Recall the step where to normalize the w value of the vector, we divide the x, y, and z value by w. Now if somewhere off screen a triangle crosses the z=0 plane then one of the rows of pixels may be divided by zero or a number that is very close to zero. This leads to a triangle much larger than the screen where each (offscreen) pixel is being calculated. To solve this problem we will clip the triangles in all directions around our (1,1,1)-(-1,-1,-1) box. We would end up with a lot of duplicated code writing this function for each of the 6 clipping planes so instead we will write a more general function for clipping and apply it 6 times.

There are 4 cases that we care about for a triangle intersecting a plane. I will refer to the side that will not be clipped as the “inside” of the clipping plane and the side that will be clipped as the “outside”.

1. All 3 points on the inside of the plane
2. All 3 points on the outside of the plane
3. 1 point outside and 2 points on the inside of the plane
4. 2 points outside and 1 point on the inside of the plane

The first two cases are pretty straight forward. If all 3 points are on outside, we can discard the triangle. If all 3 points are on the inside, we can keep the triangle. Case number 3 requires us to split the visible part of the triangle into two pieces. The input triangle is shown in red and the output triangles are shown in green:

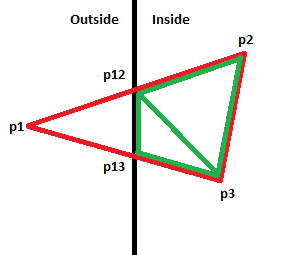
And case number 4 can be resolved by replacing the triangle with one that has the two outside vertices moved to the boundary of the plane:

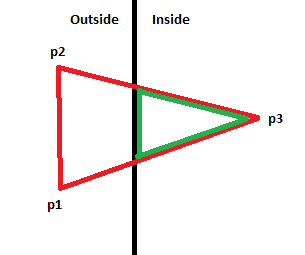
We will also need to ensure that the varyings are changed to the correct value for the new vertices. To help with this problem lets first implement a function to determine where a line segment intersects a plane. We know it must intersect the plane at some point on the segment between the two points. We will set up an equation so that a represents the percentage (0-1) that the intersection is along the segment from point 1 to point 2. For instance, if the intersection point is half way, a would be 0.5. If the intersection point is at point 1 then a would be zero and if it was at point 2 then a would be 1. The equation is based on a weighted average of the x values of the points divided by the weighted average of the w values of each point because this step will be done before the normalizeW function is called. Then I set that equation equal to 1 which is the x position of the plane we are checking for. This equation can also be solved for y and z and for the planes located at -1 as well.

(x1*(1-a) + x2*a) / (w1*(1-a) + w2*a) = 1

Solving this equation for a, we get:

a = (x1-w1) / ((w2-w1)-(x2-x1))

Now that we have the value to interpolate between, we just need to generate a vertex at each intersection of a triangle’s line segments and use those to construct a new triangle or triangles that are entirely inside the rendering area. We can also interpolate all of the varyings in the same way we interpolate the spatial coordinates. To avoid duplicating code, we will write a function that takes two callback functions. One callback will return the coordinate’s distance from the plane (positive means inside, negative means outside). We can use this callback to determine which vertices are on which side of the clipping plane. The other callback function will return the equation above computed for the coordinate and side (+/- 1) of the cube. This will tell us where the edges of the triangle intersect the plane as an interpolated value between vertices. Below are the functions for each clipping plane:

let getPlaneIntersection = (aX, aW, bX, bW, val) => {
	return (aX - (aW * val)) / ((bW - aW) * val + aX - bX);
}

getAPX = (pA, pB) => getPlaneIntersection(pA.x, pA.w, pB.x, pB.w, 1);
getANX = (pA, pB) => getPlaneIntersection(pA.x, pA.w, pB.x, pB.w, -1);
getAPY = (pA, pB) => getPlaneIntersection(pA.y, pA.w, pB.y, pB.w, 1);
getANY = (pA, pB) => getPlaneIntersection(pA.y, pA.w, pB.y, pB.w, -1);
getAPZ = (pA, pB) => getPlaneIntersection(pA.z, pA.w, pB.z, pB.w, 1);
getANZ = (pA, pB) => getPlaneIntersection(pA.z, pA.w, pB.z, pB.w, -1);

let getPX = (p) => 1 - p.point.x / p.point.w;
let getPY = (p) => 1 - p.point.y / p.point.w;
let getPZ = (p) => 1 - p.point.z / p.point.w;
let getNX = (p) => p.point.x / p.point.w + 1;
let getNY = (p) => p.point.y / p.point.w + 1;
let getNZ = (p) => p.point.z / p.point.w + 1;

In the naming convention I used P and N for positive and negative sides of the cube, X, Y, and Z for the axis, and A for the functions that return the A value in the equation above. The getPlaneIntersection function is a more generalized version of the function above where I replaced the 1 with value so it could be used for planes at +1 and -1.

For the clipping function, we will accept an array of triangles, and two callback functions. getV will be our callback function that we use to determine what side of the plane a vertex is on. getA will be the function that we use to calculate the a value given two points. The function should return a new list of triangles, leaving out triangles that are outside the plane, and clipping other triangles to keep only the parts inside the plane. The code below shows the logic for removing triangles completely outside the plane, keeping triangles completely inside the plane, and leaving a place to compute the clipped triangles that are some mixture of the two:

function clipTriangles(tris, getV, getA) {
	let ret = [];
	for (let i = 0; i < tris.length; i++) {
		let tri = tris[i];
		//values less than 0 are outside the plane
		let p1b = (getV(tri.p1) < 0);
		let p2b = (getV(tri.p2) < 0);
		let p3b = (getV(tri.p3) < 0);
		
		p1b = p1b || tri.p1.point.w <= 0;
		p2b = p2b || tri.p2.point.w <= 0;
		p3b = p3b || tri.p3.point.w <= 0;
		
		if (!p1b && !p2b && !p3b) {
			ret.push(tri);
			continue;
		}
		if (p1b && p2b && p3b) {
			continue;
		}
		// If we reach this point, the triangle intersects
		// the plane and needs to be clipped
	}
	return ret
}

Now to clip the triangles we need to determine if the triangle has one or two vertices outside the plane. The logic below does this as well as “rotating” the vertices so that the one or two vertices outside the clipping plane end up as p1 and p2.

let twoBehind = false;
if (p2b && !p1b) {
	//rotate left
	let tmp = tri.p1;
	tri.p1 = tri.p2;
	tri.p2 = tri.p3;
	tri.p3 = tmp;
	twoBehind = p3b;
} else if (p3b && !p2b) {
	//rotate right
	let tmp = tri.p3;
	tri.p3 = tri.p2;
	tri.p2 = tri.p1;
	tri.p1 = tmp;
	twoBehind = p1b;
} else {
	twoBehind = p2b;
}

if (twoBehind) {
	//first two verts are getting clipped
	//results in one triangle
} else {
	//only the first vert is getting clipped
	//results in two triangles
}

The variable twoBehind now tells us if the first two vertices are behind the clipping plane. If twoBehind is false then the first vertex is the only one behind the clipping plane.

To cover the first case of two vertices being behind the clipping plane, we need to modify the triangle by moving the first two vertices up to the edge of the plane. Fortunately we can do this using our getA function to calculate how much to interpolate between the points. We need a for both p1-p3 and p2-p3 since both segments intersect the plane.

let tA = getA(tri.p1.point, tri.p3.point);
let tB = getA(tri.p2.point, tri.p3.point);

Then we can use both of these values to linearly interpolate the vertex and varying’s positions:

tri.p1.point = tri.p1.point.scale(1-tA).add(tri.p3.point.scale(tA));
tri.p2.point = tri.p2.point.scale(1-tB).add(tri.p3.point.scale(tB));
for (let i = 0; i < tri.p1.varyingArray.length; i++) {
	tri.p1.varyingArray[i] = tri.p1.varyingArray[i] * (1 - tA) + tri.p3.varyingArray[i] * tA;
	tri.p2.varyingArray[i] = tri.p2.varyingArray[i] * (1 - tB) + tri.p3.varyingArray[i] * tB;
}
ret.push(tri);

Notice that to do the linear interpolation, we need to add the scale function to our Point4 class to run the code above:

scale(s) {
	return new Point4(this.x * s, this.y * s, this.z * s, this.w * s);
}

The second case can be covered in a similar way. First we get the a values between p1-p2 and p1-p3.

let tA = getA(tri.p1.point, tri.p2.point);
let tB = getA(tri.p1.point, tri.p3.point);

This time we need to create new vertices after interpolating since we will have to make new triangles:

let p12 = tri.p1.point.scale(1-tA).add(tri.p2.point.scale(tA));
let p13 = tri.p1.point.scale(1-tB).add(tri.p3.point.scale(tB));
let v12var = new Array(tri.p1.varyingArray.length);
let v13var = new Array(tri.p1.varyingArray.length);
for (let i = 0; i < tri.p1.varyingArray.length; i++) {
	v12var[i] = tri.p1.varyingArray[i] * (1 - tA) + tri.p2.varyingArray[i] * tA;
	v13var[i] = tri.p1.varyingArray[i] * (1 - tB) + tri.p3.varyingArray[i] * tB;
}
let v12 = new Vertex(p12, null, v12var);
let v13 = new Vertex(p13, null, v13var);

Then we can create our two triangles with the new vertices and add them to the list:

let tri1 = new Triangle(v12.clone(), tri.p2.clone(), tri.p3.clone());
let tri2 = new Triangle(v12, tri.p3.clone(), v13);

ret.push(tri1, tri2);

The code above needs to clone vertices to prevent modifications to the varying values from affecting other triangles. Here is the clone method I added to the vertex class:

clone() {
	return new Vertex(this.point.clone(), this.attributes, this.varyingArray.slice(0));
}

Now we can modify our drawTriangles function to clip all triangles that are passed to it. As we clip triangles, we can pass the previously clipped triangles to the next clipping function until we have the final list:

function drawTriangles(buffer, triangles, vertexShader, fragmentShader, uniforms) {
	for (let i = 0; i < triangles.length; i++) {
		let t = triangles[i];
		let tNext = new Triangle();
		tNext.p1 = vertexShader(t.p1, uniforms);
		tNext.p2 = vertexShader(t.p2, uniforms);
		tNext.p3 = vertexShader(t.p3, uniforms);
		
		let tris = clipTriangles([tNext], getNZ, getANZ, true);
		tris = clipTriangles(tris, getPZ, getAPZ);
		
		tris = clipTriangles(tris, getPX, getAPX);
		tris = clipTriangles(tris, getNX, getANX);
		
		tris = clipTriangles(tris, getPY, getAPY);
		tris = clipTriangles(tris, getNY, getANY);
		
		for (let j = 0; j < tris.length; j++) {
			drawTriangle(buffer, tris[j], fragmentShader, uniforms);
		}
	}
}

The demo that would slow to a halt before now should run relatively smoothly. When the plane intersects the camera things can still get a bit slow depending on your browser and cpu. This is mainly due to the entire screen being filled with pixels combined with the relatively slow fill rate of our software renderer. The renderer could be optimized further or written in another language with threading support, however in the next tutorial we will continue by adding texture sampling and demoing several common shaders rewritten for our software renderer!

Start

Tweet Share